How to calculate Z-score and probability
What is Z Score :
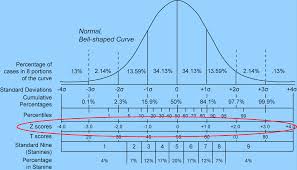
Some statistical tests are used more commonly than the Z score. The Z score is a very simple means of standardizing the distribution of a collection of numerical values that describe a “population”. Assuming that these numbers are distributed symmetrically around their average (or “normal”), you can convert any number from that population that is included in the Z score. The Z score is the number of deviations from that value that come from that population average. When you get the Z-score amount, you can use a standard table to find the probability of the highest or lowest occurrence values.
Z-score and probability calculation
Step 1
It measures the trait of interest in the population you are studying. As an example, consider a class of 100 students (the population) taking a test. You would have to collect the marks (the trait of interest) from the 100 students who take the test.
Step 2
Calculate the average (or “mean”) value of the trait of interest for your population. This is done by adding all the measured values and dividing the number of values. The average test score of 73.8 percent will be used for this example.
Step 3
Calculate the standard deviation, sigma, for the population. This can be done by hand but it is much easier to find the sigma using a standard scientific calculator or program software like Excel. The standard deviation is a measure of the amount of variation, or extent, in population values. The sigma value to be used in the test scores example is 8.6 percent.
Step 4
Determine the value of the population trait for which you want to calculate a probability. The Z test will give you the probability to find a trait in the population that can be higher or lower than the value you chose. For test scores, assume you want to know the probability that a student will score 90 percent or higher on the test, so that the value you choose is 90.
Step 5
Calculate the Z-score for the value you chose. This is done by subtracting the value you chose from the population average, then dividing that difference by the sigma of your population. So the Z score for a 90 percent brand would be equal to (90 – 73.8) / 8.6 = 1.88.
Step 6
Check your Z-score calculation on a standard Z-value table. To do this, scroll down the left column of the table until you find a value equal to the first two digits of your Z score (1.8 in the example). This locates the row you are going to use. Look along the top row until you find a value equal to the second decimal digit of your Z score (0.08 in the example). This locates the column you are going to use. Where your column and row intersect, read the numerical value at that location. In the sample test, a Z score of 1.88 corresponds to a reading of 0.4699. This number is the probability (in decimal form) of finding a student who has a test score between the average score and the value you chose of 90 percent.
Step 7
Subtract the probability you just determined from 0.50. This is necessary because table Z always gives the probability of finding a value between the middle and the value you chose and instead of wanting to know the probability of exceeding the value you chose. The reason for subtracting 0.50 is that the total probability of any score, on the one hand, is 50 percent. For the example, the value you would have to calculate would be 0.50 – 0.4699 = 0.0301.
Step 8
Multiply the number you just calculated by 100. This is the probability percentage of the value found in the population at and above the value you chose. So, the probability of any student achieving 90% of the score or higher is 3.01 percent. The probability of a brand less than 90% would be 100 minus this value or 96.99 percent.
One type of problem that is typical in an introductory statistics course is getting a z-score for some value of a normally distributed variable. Having argued for this, we will see several examples of this type of performance of computation.
The reason for the z-score
There are an infinite number of normal distributions. There is also a standard normal distribution. The goal of a computation relates a particular normal distribution to the z-score standard normal distribution. The standard normal distribution has been well studied, and there is a state of tables, which we can then use for applications to provide the area below. Due to this universal use of the standard normal distribution, it becomes a worthwhile attempt to standardize a common variable. All that this z-score means is the number of standard deviations that we are far from the mean of our distribution.
Formula of Z score :
The formula that we will use is as follows: Z = (x – μ) / σ
Each part of the formula describes:
- X is the value of our variable
- μ is the mean of the value of our population.
- σ is the value of the standard deviation of the population.
- z is z -score.
Examples of Z score
Now we will consider several examples that illustrate the use of the z -score formula. Suppose we are aware of a population of a particular breed of cats that are normally distributed. Furthermore, we know that the mean of the distribution is 10 pounds and the standard deviation appears to be 2 pounds.
Consider the following questions:
- What is Z -score for 13 pounds?
- What is z -score for 6 pounds?
- How many pounds corresponds to a -score of Z 1.25?
For the first question, we simply plug x into our = 13 z -score formula. the result is:
(13 – 10) / 2 = 1.5
This means that 13 means above one and a half standard deviations.
The second is similar to the question. Simply plug x in our formula = 6. The result for this is:
(6 – 10) / 2 = -2
The explanation of this is that 6 means below is two standard.
For the last question, we now z -score our address. For this problem we plug in the formula z = 1.25 and use algebra to solve for x:
1.25 = (x – 10) / 2
Multiply both sides by 2:
2.5 = (x – 10)
10 Add both sides:
12.5 = x
And so we see that 12.5 pounds corresponds to a -score of Z 1.25.