Maharashtra board Science Part 1 Class 10 Chapter 1 Gravitation Solutions
Science Part I Solutions for Class 10 Science Chapter 1 – Gravitation Pdf Free download:
- The phenomenon of gravitation was discovered by Sir Isaac Newton. As the story goes, he discovered the force by seeing an apple fall from a tree on the ground.
- He wondered why all apples fall vertically downward and not at an angle to the vertical. Why do they not fly off in a horizontal direction?
- After much thought, he came to the conclusion that the earth must be attracting the apple towards itself and this attractive force must be directed towards the center of the earth.
- The direction from the apple on the tree to the center of the earth is the vertical direction at the position of the apple and thus, the apple falls vertically downwards.
- A force acts on any object moving along a circle and it is directed towards the centre of the circle is called the Centripetal force. `Centripetal’ means centre seeking.
- Planetary motion had been observed by astronomers since ancient times. Before Galileo, all observations of the planet’s positions were made with naked eyes.
- By the 16th century a lot of data were available about planetary positions and motion. Johannes Kepler, studied these data.
- He noticed that the motion of planets follows certain laws. He stated three laws describing planetary motion.
Class 10 Science Chapter 1 Gravitation Exercise Solutions :
Question 1: Study the entries in the following table and rewrite them putting the connected items in a single row.
| I | II | III |
|---|---|---|
| Mass | m/s² | Zero at the Centre |
| Weight | Kg | Measure of Inertia |
| Acceleration due to gravity | nm²/kg² | Same in the entire universe |
| Gravitational Constant | N | Depends on hight |
Answer :
Study the entries in the following table and rewrite them putting the connected items in a single row
| I | II | III |
|---|---|---|
| Mass | Kg | Zero at the Centre |
| Weight | N | Measure of Inertia |
| Acceleration due to gravity | m/s² | Same in the entire universe |
| Gravitational Constant | nm²/kg² | Depends on hight |
Question 2: Answer the following questions.
a. What is the difference between mass and weight of an object. Will the mass and weight of an object on the earth be same as their values on Mars? Why?
Answer :
Mass. Weight
1.Mass is the amount weight is the force
of matter contained exerted on a body
in a body. Such as earth ,the sun and the moon.
2. Mass is the intrinsic weight is extrinsic
property of a body property of a body.
3.The mass of a body The weight of body
Cannot be zero. Can be zero.
4.mass is the measure weight is the of inertia. Measure of force.
5. The mass of a body The weight of a body
remains the same depends on the local
everywhere in the acceleration due to
Universe. gravity where it is placed.
6. The SI unit of mass SI unit is Newton (N)
is kilogram(kg).
7.The mass of a body The weight of a body
Can be measured can be measured
Using a beam using a spring balance
balanced and and a weighing
pan balance machine.
The mass of an object on the Earth will be same as that on Mars but its weight on both the planets will be different. This is because the weight (W) of an object at a place depends on the acceleration due to gravity of that place i.e. W=mg or W∝gW=mg or W∝g and since the values of acceleration due to gravity on both the planets differ, thus the weight of the object will be different for both the planets.
b. What are (i) free fall, (ii) acceleration due to gravity (iii) escape velocity (iv) centripetal force ?
Answer :
c. Write the three laws given by Kepler. How did they help Newton to arrive at the inverse square law of gravity?
Answer :
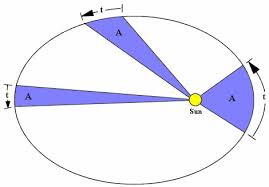
First Law: The orbits of the planets are in the shape of ellipse, having the Sun at one focus.
Second Law: The area swept over per hour by the radius joining the Sun and the planet is the same in all parts of the planets orbit.
Third Law: The squares times of the planets are proportional to the cubes of their mean distances from the Sun.
Newton used Kepler’s third law of planetary motion to arrive at the inverse-square rule. He assumed that the orbits of the planets around the Sun are circular, and not elliptical, and so derived the inverse-square rule for gravitational force using the formula for centripetal force. This is given as:
F = mv2/ r …(i)
F ∝ v2/ r …(ii)
Now, if the planet takes time T to complete one revolution around the Sun, then its velocity v is given as:
v = 2πr/ T …(iii)
where, r is the radius of the circular orbit of the planet
or, v ∝ r/ T …(iv) [as the factor 2π is a constant]
On squaring both sides of this equation, we get:
v2 ∝ r2/ T2…(v)
On multiplying and dividing the right-hand side of this relation by r, we get:
v2∝r3T2×1r …(vi)
According to Kepler’s third law of planetary motion, the factor r3/ T2 is a constant. Hence, equation (vi) becomes:
v2 ∝ 1/ r…(vii)
On using equation (vii) in equation (ii), we get: F∝1r2
Hence, the gravitational force between the sun and a planet is inversely proportional to the square of the distance between them.
d. A stone thrown vertically upwards with initial velocity u reaches a height ‘h’ before coming down. Show that the time taken to go up is same as the time taken to come down.
Answer :
S = h
u = u
v = 0
a = -g
Let t be the time taken by the ball to reach height h. Thus, using second equation of motion, we have
−2gh=v2−u2
⇒u=2gh−−−√Now, from first equation of motion, we have
v=u−gtt=ug=2hg−−√ …..(i)
Now, from first equation of motion, we have v=u-gtt=ug=2hg …..(i)
For vertical downward motion of the stone:
S = h
u = 0
a = g
Let v’ be the velocity of the ball with which it hits the ground. Let t’ be the time taken by the ball to reach the ground. Thus, using second equation of motion, we have
2gh=v’2⇒
v’=2gh−−√Now, from first equation of motion, we have
v’=u+gt’t’=
v’g=2hg−−√ …..
Hence, from (i) and (ii), we observe that the time taken by the stone to go up is same as the time taken by it to come down.
e. If the value of g suddenly becomes twice its value, it will become two times more difficult to pull a heavy object along the floor. Why?
Answer :
Let the mass of the heavy object be m. Thus, the weight of the object or the pull of the floor on the object is
W = mg
Now, if g becomes twice, the weight of the object or the pull of the floor on the object also becomes twice i.e. W’ = 2mg = 2W
Thus, because of doubling of the pull on the object due to the floor, it will become two times more difficult to pull it along the floor.
Question 3: Explain why the value of g is zero at the centre of the earth.
Answer : At the centre of Earth, the force due to upper half of the Earth will cancel the force due to lower half. In the similar manner, force due to any portion of the Earth at the centre will be cancelled due to the portion opposite to it. Thus, the gravitational force at the centre on any body will be 0. Since, from Newton’s law, we know
F = mg
Since, mass m of an object can never be 0. Therefore, when F = 0, g has to be 0. Thus, the value of g is zero at the centre of Earth.
Question 4: Let the period of revolution of a planet at a distance R from a star be T. Prove that if it was at a distance of 2R from the star, its period of revolution will be 8–√8 T.
Answer : From Kepler’s third law of planetary motion, we have
T2∝r3 …..(i)
Thus, when the period of revolution of planet at a distance R from a star is T, then from (i), we have
T2∝R3 …..(ii)
Now, when the distance of the planet from the star is 2R, then its period of revolution becomes T21∝(2R)3orT21∝8R3…..(iii)
Dividing (iii) by (ii), we get
T21T2=8R3 R3⇒
T1=−√ 8T.